Tuesday, November 19, 2013

Version Tracking Visualization

Results 1/21/14


Results of A/B/C/D prediction: dismal


Results 2:



Back to the CSV: class names are listed

['ant-1.3.csv', 'ant-1.4.csv', 'ant-1.5.csv', 'ant-1.6.csv', 'ant-1.7.csv']
Type A: 4%    B: 11%    C: 12%    D: 71%    NoMatch: 0%
Type A: 3%    B: 17%    C: 8%    D: 63%    NoMatch: 5%
Type A: 5%    B: 5%    C: 18%    D: 69%    NoMatch: 0%
Type A: 17%    B: 8%    C: 15%    D: 58%    NoMatch: 0%

['camel-1.0.csv', 'camel-1.2.csv', 'camel-1.4.csv', 'camel-1.6.csv']
Type A: 3%    B: 0%    C: 22%    D: 51%    NoMatch: 22%
Type A: 15%    B: 18%    C: 3%    D: 55%    NoMatch: 6%
Type A: 9%    B: 7%    C: 10%    D: 71%    NoMatch: 1%

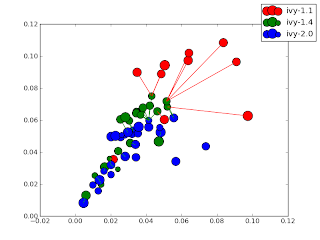
['ivy-1.1.csv', 'ivy-1.4.csv', 'ivy-2.0.csv']
Type A: 7%    B: 47%    C: 2%    D: 40%    NoMatch: 1%
Type A: 0%    B: 0%    C: 0%    D: 0%    NoMatch: 100%

['jedit-3.2.csv', 'jedit-4.0.csv', 'jedit-4.1.csv', 'jedit-4.2.csv', 'jedit-4.3.csv']
Type A: 17%    B: 15%    C: 5%    D: 58%    NoMatch: 2%
Type A: 16%    B: 7%    C: 9%    D: 62%    NoMatch: 4%
Type A: 9%    B: 15%    C: 3%    D: 64%    NoMatch: 6%
Type A: 0%    B: 11%    C: 0%    D: 47%    NoMatch: 38%

['log4j-1.0.csv', 'log4j-1.1.csv', 'log4j-1.2.csv']
Type A: 16%    B: 6%    C: 8%    D: 41%    NoMatch: 27%
Type A: 30%    B: 1%    C: 56%    D: 5%    NoMatch: 5%

['lucene-2.0.csv', 'lucene-2.2.csv', 'lucene-2.4.csv']
Type A: 33%    B: 12%    C: 24%    D: 28%    NoMatch: 1%
Type A: 42%    B: 15%    C: 21%    D: 15%    NoMatch: 4%

['synapse-1.0.csv', 'synapse-1.1.csv', 'synapse-1.2.csv']
Type A: 5%    B: 4%    C: 22%    D: 63%    NoMatch: 3%
Type A: 13%    B: 12%    C: 19%    D: 53%    NoMatch: 1%

['velocity-1.4.csv', 'velocity-1.5.csv', 'velocity-1.6.csv']
Type A: 40%    B: 34%    C: 2%    D: 2%    NoMatch: 20%
Type A: 26%    B: 37%    C: 3%    D: 29%    NoMatch: 2%

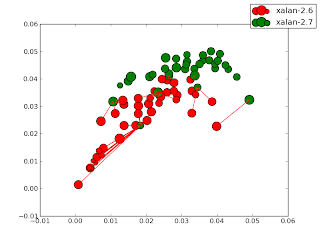
['xalan-2.4.csv', 'xalan-2.5.csv', 'xalan-2.6.csv', 'xalan-2.7.csv']
Type A: 9%    B: 4%    C: 36%    D: 44%    NoMatch: 4%
Type A: 27%    B: 20%    C: 15%    D: 31%    NoMatch: 4%
Type A: 44%    B: 0%    C: 51%    D: 1%    NoMatch: 2%

['xerces-1.2.csv', 'xerces-1.3.csv', 'xerces-1.4.csv']
Type A: 3%    B: 11%    C: 10%    D: 72%    NoMatch: 1%
Type A: 7%    B: 0%    C: 38%    D: 25%    NoMatch: 27%

Idea: New dataset consisting of:

  • All attributes of N
  • All attributes of N+1
  • The delta between N and N+1
  • Class of defect change

Result1


  • Preliminary feature selection with info gain selecting top 50%
  • Normalized and discredited with Fayyed-Irani
  • PCA via FastMap
  • Grid clustering
  • Centroids plotted along with version n+1 nearest neighbor lines. (Not terribly useful)
  • Do I smell transforms of best fit around the corner?











Results0

k-means 5 to cluster each data-set within itself
Eigenvalues used to determine select features with most influance
Actual selected columns are plotted, not synthesized dimensions
     -- significant correlations could be reported as synonmyms
rules for connecting the dots?







Posted by at No comments:
Labels:

Monday, November 11, 2013

Tree query languages for MOEA

Method

  1. Cluster the data
  2. Find deltas of interest between the clusters
    • Score each cluster
      • Let each row have objective scores, normalized 0..1, min..max
      • Let the score of a row by the sum of the normalized scores
      • Let the score of a cluster be the mean of the score of its rows
      • Technically, this is almost the cdom predicate used in IBEA
    • For each cluster C1
      • Find its nearest neighbor C2 with a better score 
      • Assert one  (leave,goto)  tuple for  (C1,C2)
  3. Build and prune a decision tree on the clusters
    • Label each instance with the cluster it belongs to
    • Build a decision tree on the labelled data set.
    • Find the clusters that are only weakly recognized by the decision tree learner
      • e.g. use a three-way cross val and prune anything with F < 0.5
    • Remove the weakly recognized clusters
  4. For each (C1,C2) tuple where both are not weakly recognized, 
    • Query the tree to find the delta
Observation: the trees are so small that this can be done manually.

Example

Nasa93 clustered into 2D (one color per cluster)

Cluster details 
  • All the following values are normalized 0..1, min..max
  • Defects and months are connected, but not always
  • Effort is not what separates the projects- its more about defects and calender time to develop
  • Clearly, cluster 2 is a bad place and 10 and 13 look nicest.


A decision tree learned from the data labelled with each cluster (ignoring the objectives) generated:

 acap = h
|   apex = h
|   |   pmat = h
|   |   |   plex = h: _2 (6.0/1.0)
|   |   |   plex = n: _4 (3.0)
|   |   pmat = l
|   |   |   cplx = vh: _3 (2.0)
|   |   |   cplx = h
|   |   |   |   time = vh: _3 (3.0)
|   |   |   |   time = n: _6 (4.0/1.0)
|   |   |   cplx = n: _5 (2.0)
|   |   pmat = n: _6 (4.0/1.0)
|   apex = n
|   |   data = h: _6 (2.0/1.0)
|   |   data = n: _4 (3.0/1.0)
|   |   data = l: _13 (1.0)
|   apex = vh
|   |   pcap = h: _10 (3.0)
|   |   pcap = vh: _7 (2.0/1.0)
acap = n
|   sced = n
|   |   stor = xh: _7 (1.0)
|   |   stor = n
|   |   |   cplx = h
|   |   |   |   pcap = h: _10 (3.0/1.0)
|   |   |   |   pcap = n: _13 (3.0)
|   |   |   cplx = n: _7 (3.0/1.0)
|   |   stor = vh: _11 (3.0)
|   |   stor = h: _11 (2.0)
|   sced = l
|   |   $kloc <= 16.3: _9 (5.0)
|   |   $kloc > 16.3: _8 (6.0)
acap = vh: _12 (7.0/1.0)

A 3-way cross-val yielded following confusion matrix. 
  • The underlined and bold entries are the correctly classified rows.
  • The red entries are errors.
  •  Note the poor performance for recognizing clusters 4,5,6,7,10,13

 a b c d e f g h i j k l   <-- as="" classified="" font="">
 5 0 0 0 0 0 0 0 0 0 0 0 | a = _2
 0 4 1 1 0 0 0 0 0 0 0 0 | b = _3
 1 0 2 0 1 0 0 0 1 0 0 0 | c = _4
 0 1 1 0 3 0 0 0 0 0 0 0 | d = _5
 0 1 2 3 0 0 0 0 1 0 0 1 | e = _6
 0 0 0 0 0 0 0 0 1 2 1 1 | f = _7
 0 0 0 0 0 0 6 0 0 0 0 0 | g = _8
 0 0 0 0 0 0 1 4 0 0 0 0 | h = _9
 0 0 1 0 0 0 0 0 3 0 0 2 | i = _10
 0 0 0 0 0 1 0 0 0 4 0 0 | j = _11
 0 0 0 0 0 1 0 0 0 0 6 0 | k = _12
 0 0 1 0 0 0 0 0 1 1 0 2 | l = _13


The above confusion matrix is mapped into the "f" measures of the following table. 
  • The "goto" column marks the deltas of interest.
  •  Low "f" values are marked in gray. 
  • Any "goto" that comes or goes into gray is marked with gray.

cluster n effort defects months f     goto
2 5 43% 25% 72% 91% 3
3 6 5% 32% 42% 67% 6
4 5 6% 17% 37% 31% 8
5 5 7% 29% 43% 0% 6
6 8 6% 24% 40% 0% 10
7 5 7% 16% 36% 0% 13
8 6 2% 6% 17% 92% 9
9 5 0% 1% 3% 89%
10 6 2% 9% 22% 46% 12
11 5 7% 18% 31% 67% 13
12 7 2% 7% 18% 86%
13 5 7% 15% 26% 36%
total: 68




 
If we prune the above tree of any branch that leads only to gray classes, we get, as promised above, a very small tree.

acap = h
|   apex = h
|   |   pmat = h
|   |   |   plex = h: _2 (6.0/1.0)
|   |   pmat = l
|   |   |   cplx = vh: _3 (2.0)
|   |   |   cplx = h
|   |   |   |   time = vh: _3 (3.0)
acap = n
|   sced = n
|   |   stor = vh: _11 (3.0)
|   |   stor = h: _11 (2.0)
|   sced = l
|   |   $kloc <= 16.3: _9 (5.0)
|   |   $kloc > 16.3: _8 (6.0)
acap = vh: _12 (7.0/1.0)

Summary

  • The definite statements that clearly make changes in SE data are very succinct.
    • But they might not cover everything.
Question: what would you baseline this against? I.e. how would you certify this as a good/crappy idea?
Posted by at No comments:
Subscribe to: Posts (Atom)