Text Mining

Recently, Ourmine was used to perform a large text mining experiment on the following large data sets:

Express schemas: AP-203, AP-214
BBC, BBC Sport
Reuters 
The Guardian, (multi-view text data sets)
20 Newsgroup subsets
The main purpose of the experiment was to determine the overall benefits of using slow clustering/dimensionality reduction methods over heuristic means. To conduct the experiment, two dimensionality reduction methods were used - Tf*Idf and PCA - in conjunction with three clustering methods (a naive K-means, GenIc, Canopy clustering).

Tf*Idf, or term frequency * inverse document frequency, is a fast reduction method that reduces the number of attributes in a text data set by filtering out important terms from unimportant ones. The concept here is to identify the terms that appear frequently in a small number of documents, and infrequently across the entire corpus. This allows us to evaluate how "relevant" terms are to that particular document pertaining to a specific concept.

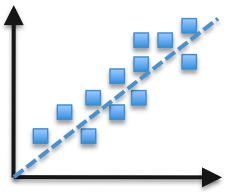
PCA, or Principal Components Analysis, is a reduction method that treats every instance in a dataset as a point in N-dimensional space. PCA looks for new dimensions that better fit these points. In more mathematical terms, it maps possibly correlated variables into a smaller set of uncorrelated variables, which are called principal components. The following image shows an example of how two dimensions can be approximated in a single new dimension feature, as seen by the dashed line.



K-means is a very slow clustering method used (in this experiment) to cluster documents from each corpus.  It's a special case of a class of EM algorithms, works as follows:

Select initial {\em K} centroids at random;
Assign each incoming point to its nearest centroid;  
Adjusts each cluster's centroid to the mean of each cluster;
Repeat steps 2 and 3 until the centroids in all clusters stop moving by a noteworthy amount;
GenIc is a single-pass, stochastic (fast) clustering algorithm. It begins by initially selecting K centroids at random from all instances in the data. At the beginning of each generation, set the centroid weight to one. When new instances arrive, nudge the nearest centroid to that instance and increase the score for that centroid. In this process, centroids become "fatter" and slow down the rate at which they move toward newer examples. When a generation ends, replace the centroids with less than X percent of the max weight with N more random centroids. Repeat for many generations and return the highest scoring centroids.
Canopy clustering is another heuristic clustering method. Developed by Google, canopy clustering reduces the need for comparing all items in the data using an expensive distance measure, by first partitioning the data into overlapping subsets called "canopies". Canopies are first built using a cheap, approximate distance measure. Then, more expensive distance measures are used inside of each canopy to cluster the data. 
Results
In order to determine the benefit of using each clustering method, cluster purity and similarity are used. When a document's class is given to us, we can determine a cluster's purity by finding how "pure" a cluster is based on the existence of classes per cluster. For instance, if a cluster contains a large number of documents containing a large number of classes, the purity of that cluster is relatively low. However, if a cluster contains a large number of documents with very few classes, we can say that the cluster has a high purity.
Cluster similarity tells us how similar documents are either within (intra-cluster similarity) a cluster, or across many clusters (inter-cluster similarity). Thus, we strive for a very high intra-cluster similarity, but a very low inter-cluster similarity based on the concept that clusters are meant to group documents together based on how "similar" they are, therefore we don't want a clustering solution to group documents together that are in no way similar to one another.
The results of this experiment are astounding. The following table represents cluster similarities in relation to runtimes normalized to the more rigorous methods (as these were assumed to perform the best).


Reducer and Clusterer
Time
Intersim
Intrasim
Gain
TF-IDF*K-means
17.52
-0.085
141.73
141.82
TF-IDF*GenIc
3.75
-0.14
141.22
141.36
PCA*K-means
100.0
0.0
100.0
100.0
PCA*Canopy
117.49
0.00
99.87
99.87
PCA*GenIc
11.71
-0.07
99.74
99.81
TF-IDF*Canopy
6.58
5.02
93.42
88.4
 

In this table, "Gain" is the value of the intra-cluster similarity minus the value of the inter-cluster similarity. Thus, a higher gain represents a better overall score for that particular clusterer and reducer. As can be seen, most methods lie below the more rigorous methods (PCA*K-means). However, TF-IDF produces better results than does PCA on most combinations, and by observing TF-IDF*GenIc, we can see that even though is scores second in the table, its runtime is about 1/5-th that of TF-IDF*K-means.
Links to graphs of overall weighted cluster purities are found below for the BBC and BBCSport data sets.  As we can see, in BBCSport, slower methods (K-means) provides the highest cluster purity. However, in BBC we can see that GenIc gives us results that are very close to those of slower solutions. 
BBC purities 
BBC Sport purities