WMC3 - CDA
Recap Problem Statement: We're trying to use GALE to make safety-critical decisions in short time. We're using the CDA model from WMC3, built by Georgia Tech scholars, to learn what organizational structures within the cockpit (in terms of how the pilots should handle their taskload) best optimize objectives such as minimizing time of delay/interruptions in getting these tasks completed. This is a cognitive science domain.
Buggy dataset: http://i.imgur.com/GCZFxie.png. Takes about 12-15 minutes to run 100 times.
Comparing to results (example: http://i.imgur.com/znv2xzv.png) from http://cci.drexel.edu/NextGenAA/pdf/jcedm-2013-Pritchett-measuring%20fa.pdf. This is our main reference paper for sanity checks on the model.
Few obvious correlations. Sanity check.
Task: Figure out the bugs. Then we can take off.
GALE
What I did:
Took away all non-determinism (random injections).
Only randomness that exists is with regeneration of individuals - but this isn't really non-deterministic (probability bin distributions).
Results: No change.
Self-reflection: we're mutating some distance, usually going too far. Then we try to come back towards it, and we go too far. Repeat, bouncing back and forth across where we want to go.
Problem: How far do we really want to bounce to get to exactly where we want to go?
Solution: Our projection axis is typically 1.0 units long. In the optimal ideal world, east = 1.0, and west = 0.0 (or vice versa). Thus absolute difference is 1.0 - 0.0 = 1.0. Taking 1 minus this, this tells us how far we need to bounce. "1 - (east - west)".
Observations: In early generations, this bounce distance is on the order of 0.30. In later generations, it's very close to 0.0. In addition, once we get close to 0.0, we STAY there.
Hypotheses: In problems that are hard to optimize, we don't get close to 0.0. Bounce distance tells us on its own how good we're doing.
New Results:
Some standard Models (Osyczka2, Vienett2, Schaffer): http://i.imgur.com/MUUC2pD.png
POM3 Models: http://i.imgur.com/aSK1gWj.png
GALE POM3B Decision Chart: http://i.imgur.com/zoL8ZiW.png
Observations: Less variance in the dots. Clearer image than before (active v6 link: http://unbox.org/things/var/joe/active/active-v6.pdf)
Tuesday, September 24, 2013
Tuesday, September 3, 2013
Noise Injection Results
BK(1) = Linear NN K=1
http://unbox.org/things/var/brian/2013/projects/data-quality/mucker2/output/9-2-2013%20plots/
Since we are still getting flat results, perhaps we should bump up the amount of noise from 0.1 - 0.5 instead of 0 - 0.4? Or even back to the 0, 0.1, 0.25, 0.5, 1 results?
http://unbox.org/things/var/brian/2013/projects/data-quality/mucker2/output/9-2-2013%20plots/
Since we are still getting flat results, perhaps we should bump up the amount of noise from 0.1 - 0.5 instead of 0 - 0.4? Or even back to the 0, 0.1, 0.25, 0.5, 1 results?
Intrinsic Dimensionality Baseline
New graph: The effect of (dataset length / critical length) on results. This was done at Q=0.7 and Rmax=len(R)/16. Shown here with 2, 3, 4, and 5 dim random data.
Simple stuff first. here's some terrible results from high-dimension random sets:
I had some problems with finding a good slope value for small datasets. The solution I found was the median of two-point slopes to a point. This seems to yield good results in places where the finite slope failed (see below).
Unique IDs crater ID. See Miyazaki94 and my modified Miyazaki2:
While staring at these graphs, I realized:
But what if you were to ignore the summation across all points and focus instead on distances from a single point (say a cluster centroid):
I also made some progress on certifying results. Smith88Intrinsic derives this relation for the minimum number of test points to show dimensionality M at range R=rmax/rmin with quality Q:
At first, the results were wild. Nmin went through the roof. By restricting R (lowering the maximum value of r which is being used to determine the ID), the ID becomes more representative of the local area and Nmin becomes reduced. (you're not making a statistical claim about as large of a sphere of influence) I set this up as a after-the fact certification envelope check on the figures. After limiting rmax to the 6.25th ptile of all distances and setting Q to 50%, the results look good (N/Nmin > 1) on most things except the effort sets that I need to re-format. If a tighter certification is needed, additional options such as tuning the parameters on a dataset-by-dataset basis is possible.
Results from Brian's Data:
note: the Lymphography dataset is not present because is not available for public download due to private data.
ecoli.csv :: 3.27
glass.csv :: 0.75
hepatitis.csv :: 2.45
iris.csv :: 1.11
labor-negotiations.csv :: 0.68
Intrinsic Dimensionality Results:
Some more progress on the paper: latest pdf
Consolidated some of my code... relevant files:
Results from revised SE effort data:
Simple stuff first. here's some terrible results from high-dimension random sets:
I had some problems with finding a good slope value for small datasets. The solution I found was the median of two-point slopes to a point. This seems to yield good results in places where the finite slope failed (see below).
Unique IDs crater ID. See Miyazaki94 and my modified Miyazaki2:
Things like dates, test fields which represent comments or notes also do nasty things. The effects of this are still visible in some of the effort datasets. I'll need to re-format the by hand to make sure it's well-conditioned if more accurate results are desired.
While staring at these graphs, I realized:
- We're seeing a spectrum of ID from extremely local to extremely global.
- The local data isn't particularly useful because you're getting an average value of all localities rather than information about a specific locality.
- The global data isn't particularly useful because as r -> max; D -> 0 (a single point)
But what if you were to ignore the summation across all points and focus instead on distances from a single point (say a cluster centroid):
- At the low end, the dimensionality of the cluster would be represented
- As r reaches the edge of the cluster, if there are other nearby clusters, the changes in D will likely be small. If there are no other clusters nearby, D will approach zero until other clusters are reached
- This could potentially be used to select a scale for visualizations or cross-project learning. (If you're going to use a 2-d map, find a subset of points with an ID close to 2.0 to maximize the amount of information conveyed.)
- This might not work, but seems intuitive. I'll do a few conceptual tests for next week.
I also made some progress on certifying results. Smith88Intrinsic derives this relation for the minimum number of test points to show dimensionality M at range R=rmax/rmin with quality Q:
At first, the results were wild. Nmin went through the roof. By restricting R (lowering the maximum value of r which is being used to determine the ID), the ID becomes more representative of the local area and Nmin becomes reduced. (you're not making a statistical claim about as large of a sphere of influence) I set this up as a after-the fact certification envelope check on the figures. After limiting rmax to the 6.25th ptile of all distances and setting Q to 50%, the results look good (N/Nmin > 1) on most things except the effort sets that I need to re-format. If a tighter certification is needed, additional options such as tuning the parameters on a dataset-by-dataset basis is possible.
Results from Brian's Data:
note: the Lymphography dataset is not present because is not available for public download due to private data.
ecoli.csv :: 3.27
glass.csv :: 0.75
hepatitis.csv :: 2.45
iris.csv :: 1.11
labor-negotiations.csv :: 0.68
Intrinsic Dimensionality Results:
ant-1.3.csv :: 3.40
ant-1.4.csv :: 3.61
ant-1.5.csv :: 2.26
ant-1.6.csv :: 2.69
ant-1.7.csv :: 2.08
ivy-1.1.csv :: 1.74
ivy-1.4.csv :: 2.67
ivy-2.0.csv :: 2.21
jedit-3.2.csv :: 2.04
jedit-4.0.csv :: 1.72
jedit-4.1.csv :: 2.03
jedit-4.2.csv :: 2.22
jedit-4.3.csv :: 2.01
log4j-1.0.csv :: 1.95
log4j-1.1.csv :: 2.67
bad file: ././arff/.svn
ant-1.7.arff :: 2.08
camel-1.0.arff :: 2.41
camel-1.2.arff :: 1.98
camel-1.4.arff :: 2.17
camel-1.6.arff :: 2.16
ivy-1.1.arff :: 1.74
ivy-1.4.arff :: 2.67
ivy-2.0.arff :: 2.21
ivy-2.0.csv :: 2.21
jedit-3.2.arff :: 2.04
jedit-4.0.arff :: 1.72
jedit-4.1.arff :: 2.03
jedit-4.2.arff :: 2.22
jedit-4.3.arff :: 2.01
kc2.arff :: 0.01
log4j-1.0.arff :: 1.95
log4j-1.1.arff :: 2.67
log4j-1.2.arff :: 2.12
lucene-2.0.arff :: 2.14
lucene-2.2.arff :: 2.69
lucene-2.4.arff :: 2.94
mc2.arff :: 1.13
pbeans2.arff :: 1.82
poi-2.0.arff :: 1.75
poi-2.5.arff :: 1.13
poi-3.0.arff :: 1.45
prop-6.arff :: 1.83
redaktor.arff :: 2.02
serapion.arff :: 0.32
skarbonka.arff :: 0.66
synapse-1.2.arff :: 1.89
tomcat.arff :: 2.76
tomcattomcat.arff :: 2.76
bad file: ././arff/too_big
velocity-1.5.arff :: 2.12
velocity-1.6.arff :: 3.00
xalan-2.6.arff :: 1.90
xalan-2.7.arff :: 1.96
xerces-1.2.arff :: 2.18
xerces-1.3.arff :: 0.00
xerces-1.4.arff :: 0.01
zuzel.arff :: 1.54
Space Dim | Mean Dimensionality | SD
5 | 4.60 | 0.10
10 | 8.37 | 0.20
15 | 11.34 | 0.13
20 | 14.64 | 0.26
25 | 16.99 | 0.26
30 | 19.30 | 1.08
35 | 22.32 | 0.58
40 | 23.71 | 0.72
 |
| Axes only |
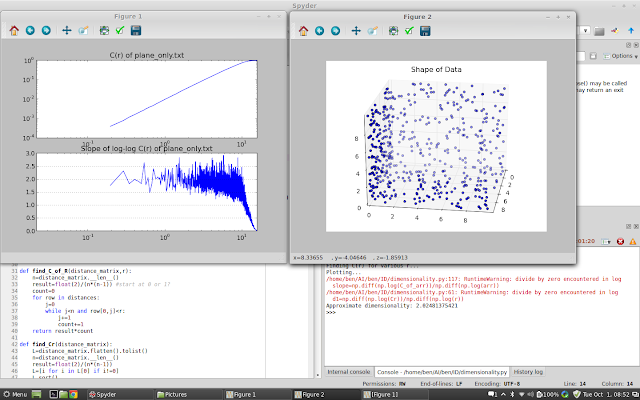 |
| Axial Planes only |

 |
| 80% Sparse 3D Dataset |
 |
| Numeric 3D Dataset |
 |
| Numberic 10D Dataset |
 |
| Numberic 100D Dataset |
UPDATE 2: PITS vs Randomized:
 |
| Original and Word-Randomized Sets of Various Length |
 |
| Original Data, Word-Randomized with Original Distribution, Word-Randomized with Uniform Distribution |
 |
| Original Data, Randomized with Original Wordcount Distribution, Randomized with Flat Wordcount Distribution |
 |
| Original, Randomized with Original Wordcount dist, Randomized with Gamma Wordcount dist |
 |
| Original and Randomized with Gamma dist Wordcounts at various Alpha |
 |
| Original and Randomized with Gamma dist Wordcounts at various Beta |
Cube of uniform distributuion (3-D):
Line of uniform distributuion (1-D):
Spiral of uniform distributuion (1-D):
Plane of uniform distributuion (2-D):
Roling Plane of uniform distribution (2-D):
Line with noise in 1-D, 2-D (line is of length 10, noise is Gaussian SD=0.1):
Subscribe to:
Posts (Atom)




































